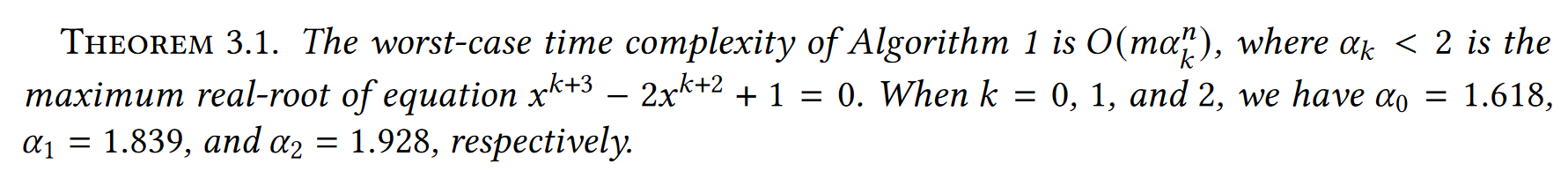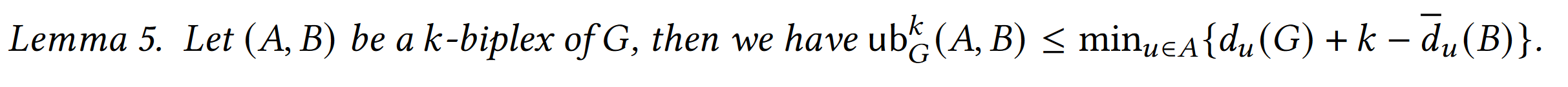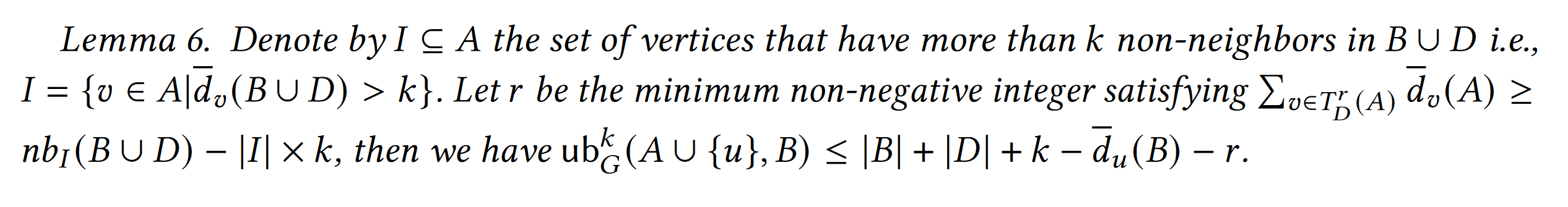论文笔记 | Efficient Maximal Biplex Enumerations with Improved Worst-Case Time Guarantee
SIGMOD 2024
QIANGQIANG DAI, RONG-HUA LI, DONGHANG CUI, and MEIHAO LIAO, YU-XUAN QIU, GUOREN WANG
1. Problem
maximal biplex enumeration
虽然是常见的问题,但是有几个难顾名思义的符号: $E_{A.B}={(u,v)\in E|u\in A, v\in B }$
2. Baseline
Baseline主要是基于一个朴素的想法,就是,在当前的biplex分支下,候选集合越小,后续的计算开销越小,所以选了个当前biplex的点在候选集合中非邻居节点最多的,从中选了个点做拓展
2.1 Algorithm
其实就是有Vertex Order
remark:
- 分支限界的表述,不太像之前的SIGMOD23的pivot框架,分支的时候,分出多个分支的那种,有点像lijun chang老师那边论文中常见的表述,分支的时候,+-某个顶点
2.2 Theorem Analysis
remark:
- m代表了每个分支,找pivot和update的时间
- 用到了经典式子,对于一个线性递推式子 $F(n)=\sum_{i=1}^jF(n-a_i)$, $F(n)$ is bounded by $O(\alpha^n)$, and $\alpha$ is the maximum real root of the equation $x^n-\sum_{i=1}^jx^{n-a_i}=0$。所以我们可以推出 $T(n)\le 2^(n/2)$,不过在本文的这种多项递推,会更复杂一些
3. Optimal Method
3.1 Pivot
remark:
- 很好理解,当$(S_L\cup C_L, S_R)$符合k-biplex定义的时候,L侧的点,除了pivot外,就没有产生分支的必要了,因为即使产生分支,pivot也可以加进去,枚举的就是所有包含pivot的maximal biplex
- 而R侧的点,如果是pivot的邻居,那加pivot也是没问题的,如果既有pivot的邻居,又没有pivot,那肯定会包含pivot的非邻居,那其实也没分支的必要了,枚举的就是包含pivot非邻居的maximal biplex
remark:
- 第一种情况很好理解,这样L侧的结果就永远不是maximal的了,就没必要枚举了,而R侧的点还是那个道理
- 第二种情况稍微复杂一点,首先R侧的点,还是那个道理,而L侧,只需要分支出Q集合,Q集合是指的是,对与pivot的任意一个非邻居u,都存在一个集合T, 使得 $(S_L\cup T, S_R\cup {u})$满足biplex,$T=C_L \setminus Q$, 那么T集合中的点的分支,肯定包含pivot的任意一个非邻居,或者Q中的点,否则就不是极大的了,前者会在R侧的分支中遍历到,后者会在Q的分支中遍历到
3.2 Algorithm
4. Optimazation Techiques
4.1 Graph Reduction
4.1.1 Core-based Reduction
经典的基于$(q_L-k,q_R-k)-core$的reduction
4.1.2 Butterfly-based Reduction
- 经典的修剪方式:k-biplex中任意两点的共同邻居数目小于对侧顶点数目减去2k
- k-biplex中任意一条边都包含在$(q-k-1)(q-2k-1)$个butterfly中
4.2 Upper Bound
假定$(X,Y)$是一个maximal k-biplex, $(A,B)$是一个k-biplex $(A,B)\in (X,Y)$.
定义:${UB}^{k}_{G}(A,B) \ge min{|X|,|Y|}$
基础的范围如下:
对于A中的一个点$u$, 它能接受的对侧顶点,最多为 $d_u(G)+(k-\overline{d}_u(B))$个 而对于A的所有点而言,它们能接受的对侧点的数目,就是所有$u$中能接受的最小的 但是这样其实挺粗糙的。
所以更精细的计算了上界。
假设一个点$u\in L$要被加入A,进行拓展
- $D={v\in N_u(G) \setminus B | (A\cup {u},B\cup {v}) is \ k-biplex}$: 也就是u被加入$(A,B)$后,它的邻居中可以用来拓展$(A,B)$的点的集合。
- $I={u\in A| \overline{d}_u(B\cup D)> k}$: 也就是如果把D全部加入拓展时,A中不满足k-biplex定义的点
- $T^{r}_{D}(A)$: r个D中拥有最多A中非邻居的顶点集合
- ${nb}_I(B\cup D)$: I中所有点在$(B\cup D)$中非邻居的数目的和
首先,根据之前宽泛的定义,我们可以得到 ${ub}G^k(A\cup{u},B)\le |B|+|D|+(k-\overline(d)_u(B))$,但是由于有I的存在,我们不可能把D全部加进去。那么肯定要去掉D中一部分点, 那么,当I中所有点额外损失的连接,都来源于$T^{r}{D}(A)$,我们把$T^{r}_{D}(A)$去了就可以,那么找个最小的r,满足图中条件,就是上界了。
如何应用呢,输入不是有q吗,如果包含当前k-biplex的结果的某条边的上限,小于q,那么就没必要枚举了,ps:理论上q越大似乎效果越好,但是结果里并不是这样的
4.3 Ordering
这个我觉得修剪力度也相当的大,其实就是之前的嵌入子图的变体版,或者说嵌入子图+分支限界的修剪,以前选择嵌入子图,是从某一侧选个点,当做初始的S集合,然后在对应的二跳子图中枚举,但是这样力度还是不够大。因为还是会枚举重复结果的二跳子图之类的情况。
干脆直接选个拥有最大度数的边,然后按照某个顺序排序好顶点之后,直接修剪成二跳且顺序更大的子图。在里面进行枚举。