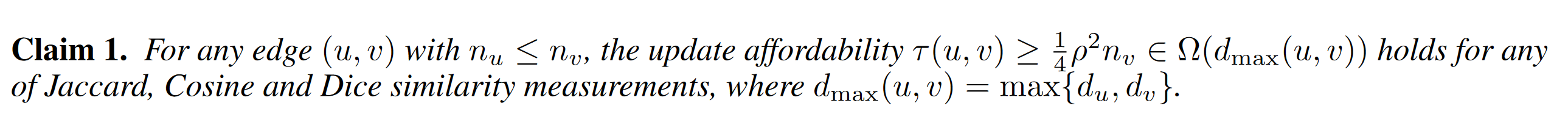论文简读 | DYNAMIC STRUCTURAL CLUSTERING UNLEASHED: FLEXIBLE SIMILARITIES, VERSATILE UPDATES AND FOR ALL PARAMETERS

arxiv的预印本，但是已被KDD 2025接收

Zhuowei Zhao , Junhao Gan, Boyu Ruan, Zhifeng Bao, Jianzhong Qi, Sibo Wang

可能是预印本的原因，感觉写的有点前后混乱，但是勉强能看懂

1. Preliminary

1.1 Problem

arxiv上预印本的问题定义有点乱，核心的问题就是，当有任意的边更新时，我们需要快速处理更新，并支持完整的SCAN查询，(输入$\epsilon$,$\mu$的那种，而不是SIGMOD 21的动态SCAN那种，给预先设置的两个参数下的结果进行更新)。 ps：其实我认为这种才是常见的动态更新维护，BOTBIN和GS-Index的更新都是这种，反而SIGMOD 21那种不太常见。

Notations $I(u,v)$: 点u和点v的共同邻居数目。

1.2 Unified Framework

包含三个结构以及对应的一些函数:

1. Sorted Neighbor Lists: 根据相似度排序的邻接表
2. EdgeSimStr: 维护所有边的相似度，包含五个函数:
   • update(u,v,op): 插入/删除后更新对应边的信息
   • insert(x,y): 插入
   • delete(x,y): 删除
   • find((u,v),op): 返回所有(u,v)能影响到的边中需要更新相似度的边(边是”invalid”的)的集合$F$
   • cal-sim(u,v): 计算相似度
3. CoreFindStr: 寻找cores, 包含两个函数:
   • update(u): 给定一个点，更新CoreFindStr
   • find-core($\epsilon$,$\mu$): 返回参数下所有cores

2. VD-STAR

2.1 Update Affordability

引入了几个概念:

• Update Affordability: $\tau(u,v)$ 表示 当前计算的相似度还能承担多少次更新, 保证$\rho-approximate$
• affordability quota: $q(u,v)=\frac{1}{4} \lfloor \tau(u,v) \rfloor_2=\frac{1}{4} 2^{\lfloor \log_2 \tau(u,v) \rfloor} \geq \frac{1}{8} \tau(u,v)$

当涉及到每个边的更新次数超过了$q(u,v)$的时候，就标记为invalid，重新计算相似度

2.2 EdgeSimStr

2.2.1 Structure

为每个点$u\in V$, 维护下面的元素：

1. $c_u$: 记录发生与$u$相关的更新事件的次数，初始为0
2. 一个排序的桶列表$B(u)$:
   • 桶的编号$i$，内部存储$q(u,v)=2^i$的邻居，$i\leq \lceil \log_2 n \rceil$
   • 非空桶按标号排序
   • 每个非空桶维护一个自己的$\overline{c}_u(B_i)$,记录自己上次被访问时$c_u$的值，初始为被加入时$c_u$的值

2.2.2 Function

1. update(u,v,op): $c_u +=1$ ，$c_v +=1$
2. insert(x,y): compute $q(u,v)$, insert vertices into buckets or create new bucket
3. delete(x,y): remove vertices from bucketes
4. find((u,v),op): 找到 $\lfloor \frac{c_u}{2^i} \rfloor > \lfloor \frac{\overline{c}_u(B_i)}{2^i} \rfloor$ 的bucket i, 遍历里面的点，将第二次被遍历的点加入$F$，第一次只做个标记 (ps:之所以这么别扭的计算来判断，主要是因为bucket加入的时候，$\overline{c}_u(B_i)$初始化为当前的$c_u$，这样就只能通过这种算法判断哪些bucket已经过了超过配额的更新次数，而第一次只做标记，似乎是为了多容纳一次更新?感觉还是会导致没达到配额极致的情况，而配额其实也是小于极限的)
5. cal-sim(u,v): 计算出一个采样次数$L$, 然后每次采样，按照抛特定概率硬币，为0就从第一个集合中取一个点，为1，就从第二个集合中取一个点，如果取的点正好在交集中，$X+=1$，然后通过特定公式计算相似度

2.2.3 Similarity Computation

证明的核心就是 概率类比频率，核心部分是这一段 (虽然按理说这样把概率当频率应该有一些误差，不知道怎么量化)：

2.2.3 proof about $\tau$

证明主要是，首先，分析单词更新，会影响到的变化的范围 然后根据计算相似度的两种情况(默认为0，或其他)下，$\tau$ 次更新后，会不会超过$rho$-approximate

3. Conlusion

• 整体感觉有点类似 SIGMOD 21年的那篇论文的相似度计算以及延迟更新策略，从jaccard拓展到其他两个相似度度量上了，然后结合了BOTBIN的思路，设计了一个 BOTBIN类似,SIGMOD 21相似度计算+延迟更新 的索引，然后包装成了一个UDF框架
• 写的有点混乱，因为是预印本？创新倒是感觉不错，值得被借鉴延迟更新，以及多个度量时的相似度计算
• 最后查询时显示比GS还快，感觉不太对劲，看了伪码，发现只输出了一个类似聚类子图的东西，没有彻底划分成一个个聚类，那确实会快一些
• 实验设置$\rho=0.02$，那么$L=8\frac{1}{\rho^2}\ln(4n^4)=80000\ln(4n)$,每次要做一次是否同时存在在另一个集合的judge，算平均度数，复杂度是$L\cdot \log d$, 邻接表做hash是$L$ .BOTBIN中bottom-k-sketch，相同$\rho$下，$k=1250\ln(2000)$ 做集合求交，快速的时间是$2k$,提前做hash是$k$， 只从相似度计算角度，bottom-k-sketch更有优势，或许从bottom-k-sketch考虑一个$\tau$和$q$，会更新更快？