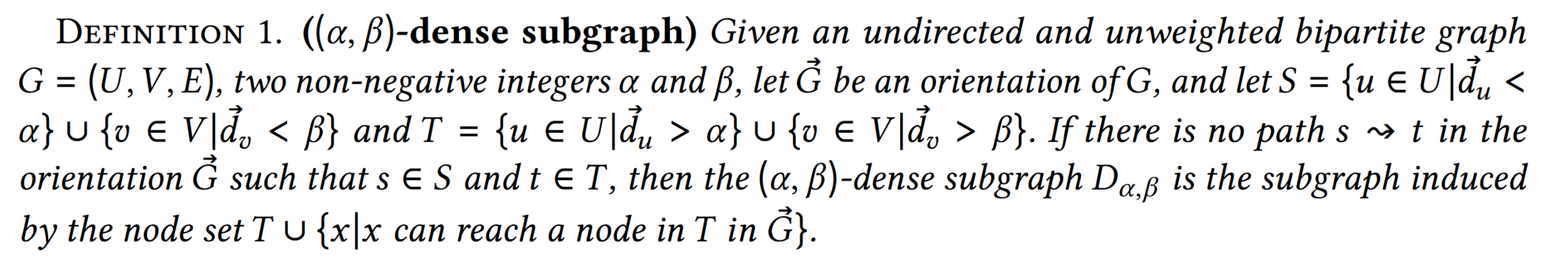论文简读 | Density Decomposition of Bipartite Graphs

SIGMOD 2025

Yalong Zhang, Rong-Hua Li, Qi Zhang, Hongchao Qin, Lu Qin, and Guoren Wang.

1.Problem Definition

1.1 motivation

1. Biclique,Biplex,Bitruss 等模型计算时间太复杂了
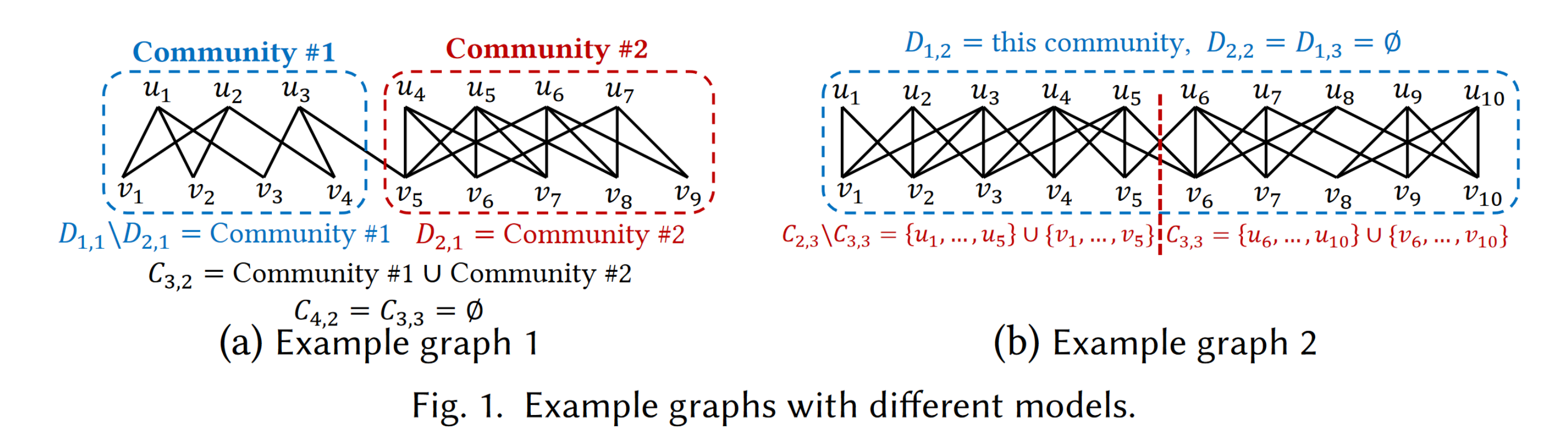
2. ($\alpha$,$\beta$)-core模型在社区识别方面不是很好，如上图所示，图a中，它无法区分两个社区，而图b中，它将同一个社区区分开了

ps:

• 所以感觉文章提出的($\alpha$,$\beta$)-dense subgraph 模型更多的似乎是用来做community search的，也就是说，可以通过不同的参数设置，区分出更加独立的社区
• 图a中的例子挺有说服力的，但是图b感觉只是core的区分可以更细，并不算缺点
• 动机是从community划分来说的，似乎做完decomposition后，实际上就是做了个图划分/聚类，和core、truss这种传统的紧密子图模型相比，肯定是优势的，甚至有点欺负人了似乎？但是不清楚和那些community detection/clustering算法相比如何，以及基于($\alpha$,$\beta$)-dense subgraph的community search和那些sota的community search算法相比如何？

1.2 notation

orientation of $G$: 给$G$里面的边分配了一个方向，将它转换成的有向图

($\alpha$,$\beta$)-dense subgraph:

ps:

• 通俗理解是将二部图转换成有向图后，划分成两部分，一部分是入度大于($\alpha$,$\beta$)的点T，一部分是入度小于($\alpha$,$\beta$)的点S，
• 如果S和T两个点集合之间没有从S到T的路径，那么子图就是T和所有能到T的点
• 更进一步的说，就是，子图就是在选定了T后，将入度等于($\alpha$,$\beta$)的点集合中能到T的点加进去，因为S集合中不能存在到T的路径
• 其实就是一次图划分，将图划分成入度小于($\alpha$,$\beta$)的点集合S和S无法影响到的入度大于等于($\alpha$,$\beta$)的点集合(假设入度代表有影响的话)

1.3 theorem about new model

1. 给定参数下，($\alpha$,$\beta$)-dense subgraph具有唯一性 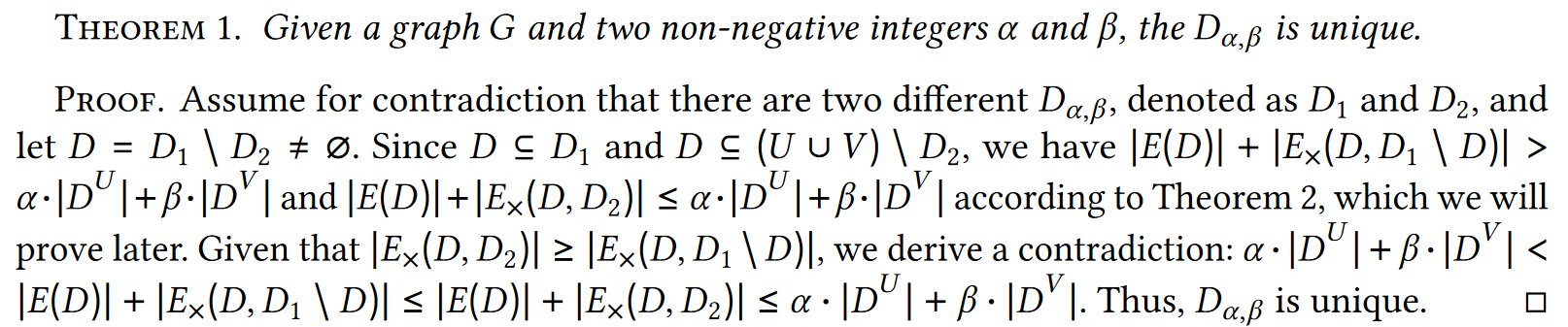ps: 证明感觉有问题，给出的反证，只能说明$|E_{\times}(D,D_2)|$<$|E_{\times}(D,D_1\setminus D)|$，并不能说明$D$并不存在
2. 满足定义的 ($\alpha$,$\beta$)-dense subgraph 有下面的特性：a. 该子图和剩下的图之间的所有的边都是出，而不是入. ps:就是定义 b. 该子图里，点在$\overrightarrow{G}$中的入度和在子图内的入度是一样的，符合($\alpha$,$\beta$)约束. ps: 因为所有的入度对应的点，都会被包含到子图里 c. 对于剩下图中的点，它的入度小于等于($\alpha$,$\beta$).
3. 当$D_{\alpha,\beta}$中任意一个集合$X$被移除，那么要损失超过$\alpha \cdot$ | $X^U$| $+\beta \cdot$ | $X^V$ | 的边，也就是说，| $E(X)$ |+| $E_\times(X,D_{\alpha,\beta}\setminus X)$ |> $\alpha \cdot$ | $X^U$ |+ $\beta \cdot$ | $X^V$ |. ps:为什么不是大于等于，是因为，如果是等于的话，说明X的入度正好等于 ($\alpha$,$\beta$),那么就既不属于S，也不属于T，而这种情况下，还正好等于 X内部+外部的边，说明它内部没有指向T的点，那就不会被包括在$D_{\alpha,\beta}$中
4. 当$D_{\alpha,\beta}$外的任意一个集合$Y$包含在内，那么要新增不超过$\alpha \cdot$ | $Y^U$ |+$\beta \cdot$ | $Y^V$ | 的边，也就是说，| $E(Y)$ |+| $E_\times(Y,D_{\alpha,\beta})$ |> $\alpha \cdot$ | $Y^U$ |+ $\beta \cdot$ | $Y^V$ |. ps:这个有等于，是因为就算Y的所有入度都是内部外部的边，正好等于 ($\alpha$,$\beta$)，也无所谓

ps: 感觉，文章漏了和1类似的引理：($\alpha$,$\beta$)-dense subgraph与orientation无关，这段话是在theorem 1之前的叙述中说的，但是我总感觉不太对劲，后面我想了一下，可能是不能划分出没有路径的S和T的orientation就得不到结果，所以需要能划分出类似的orientation，但是这样一来，oreientation的选择似乎成了一个新的问题，而且如果内部是相反的，岂不是($\alpha$,$\beta$)也是相反的了？

Remark

• density分解，有点和最密子图那个很像，类似某个参数下的“最密”子图，理论部分也有相似的感觉
• 文章故事上还是从community划分来叙述的，其实个人感觉，这样叙述的话，可能需要对比一下community search/detection(clustering)的方法。