论文笔记 | Hereditary Cohesive Subgraphs Enumeration on Bipartite Graphs: The Power of Pivot-based Approaches
SIGMOD 2023
QIANGQIANG DAI, RONG-HUA LI, XIAOWEI YE, and MEIHAO LIAO, WEIPENG ZHANG, GUOREN WANG
1. Problem Definition
Maximal Hereditary Cohesive Subgraphs Enumeration on Bipartite Graphs
Hereditary Cohesive Subgraph: 有遗传属性,实际上就是满足某个属性的子图的任何子图也满足这个属性 Maximal: 极大,就是不能再加点或边进去了,已经是约束内最大的集合了
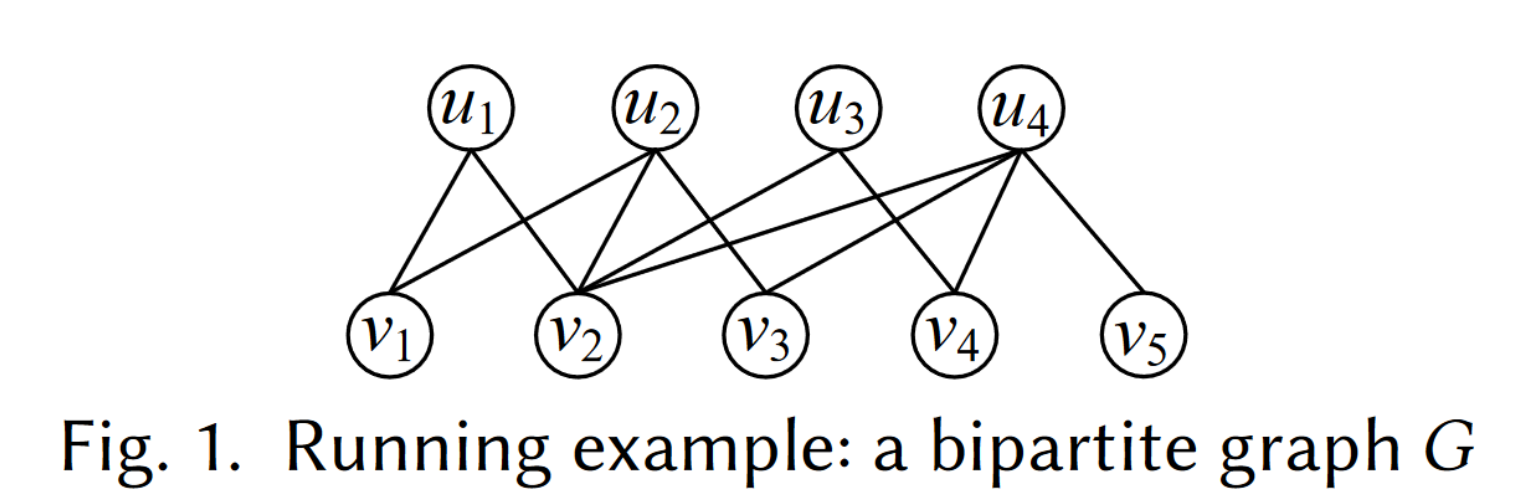
Example Graph:
2. Basic Framework
基础的分支限界枚举框架:
每次迭代遍历 R, C, X:R 是当前遍历的子图,C 是可以被放进子图中的候选点集合,X 是之前已经被用来产生分支的候选集合中的点的集合(主要是为了不重复分支和检验极大性质)。
每次分支的时候,分出|C|条分支,进入下级分支时,会根据问题的性质,从 C 和 X 中删去不可能再构成结果的点。
思考和分析:
- 假设 (A, B) 是一个结果,那分支的时候,如果 B1 分支选了 A 里的点,那 B1 分支后续子树肯定会枚举到 A。那这种时候,B2…Bn 分支如果选了 B 或 A 的其他点,那就会重复枚举 (A, B),产生冗余计算。所以如果选了一个点 v ∈ A,那么最好 A\v 和 B 中的所有点都不会再产生分支,这样就不会有任何冗余(对于 (A, B) 而言)。
3. Pivot Rule
所以考虑到上述,如果我们能选一个点作为pivot,那根据这个pivot,就可以产生一个跳过集合P,P后续就不会被选择用来产生新的分支了,那这个pivot和P需要满足:
假设选了 $u\in C_U\cup X_U$ , 那么所有的结果(A,B)都需要满足:
- A包含u
- A不包含u,但是包含起码一个$C_V\setminus P_V$中的一个点
- A不包含${u}\cup C_V \setminus P_V$中的点(不满足上述条件),但是包含起码一个$C_U\setminus (P_U\cup {u})$中的点
4. Piovt-Based Framework
- 从两侧的$C\cup X$中各选一个pivot,然后找能让跳过集合最大的pivot
- 后续分支还是一样的,就是不用跳过集合里面的点产生分支了
5. Maximal Biclique Enumeration
5.1 Pivot rule of MBCE
VLDB22年的稀疏图下极大biclique枚举的论文里,跳过集合根据dominate选的,不仅效果一般,而且算dominate也需要一些时间
本文的选择是:
- $P_U$是C中除了u以外所有的点,这个比较绕,文中给了个引理:假设后续子树涉及到的所有的包含$P_V$中的点的biclique都包含u,那么就不存在maximal biclique满足之前规则里的条件3 (A不包含${u}\cup C_V \setminus P_V$中的点,但是包含起码一个$C_U\setminus (P_U\cup {u})$中的点)。 然后根据这个引理说明我们可以这么设置$P_U$ 。我的理解是,如果设置的$P_V$ 能满足 “后续子树涉及到的所有的包含P_V中的点的biclique都包含u” 这个条件,那么$P_U$就可以这么设置。
- 根据上面的引理,如果$P_V$是u的邻居,那么就可以满足“后续子树涉及到的所有的包含P_V中的点的biclique都包含u”这个条件了。
本文这里推理出P的逻辑还是挺绕的,但是提升效果显著的地方就在这里了,其实反过来想可能会顺畅一些:
- 选择pivot主要是为了,我可以把一些会产生冗余计算的分支,不分了
- 这样的前提下,那么u的所有的邻居,都可能在包含u的maximal biclique里,所以u的所有的邻居的分支,就不分了,这样会不会引起结果缺失呢?并不会,因为如果 v是u的邻居,有个结果不包含u但是包含v,那他肯定包含u的另外一个非邻居,肯定会在u的非邻居的分支里被遍历到
- 当u的所有邻居都不分了之后,那其实剩下的所有的$C_U$都可以不分了,假设有个结果不包含u,也不包含u的非邻居,但是包含$C_U\setminus{u}$,那他肯定不是结果,否则一定要包含u(也就是会在u的后续子树里被遍历),要么一定包含 u的非邻居(也就是会在 $v\in C_V\setminus N(u)$ 的分支里被遍历)。
感觉和之前的相比,最大的区别就是$P_U$了,别的方法大部分可能不管二跳邻居就行了,但是实际上,选了pivot了之后,同侧所有其他顶点都可以先不分支。
5.2 Time complexity analysis
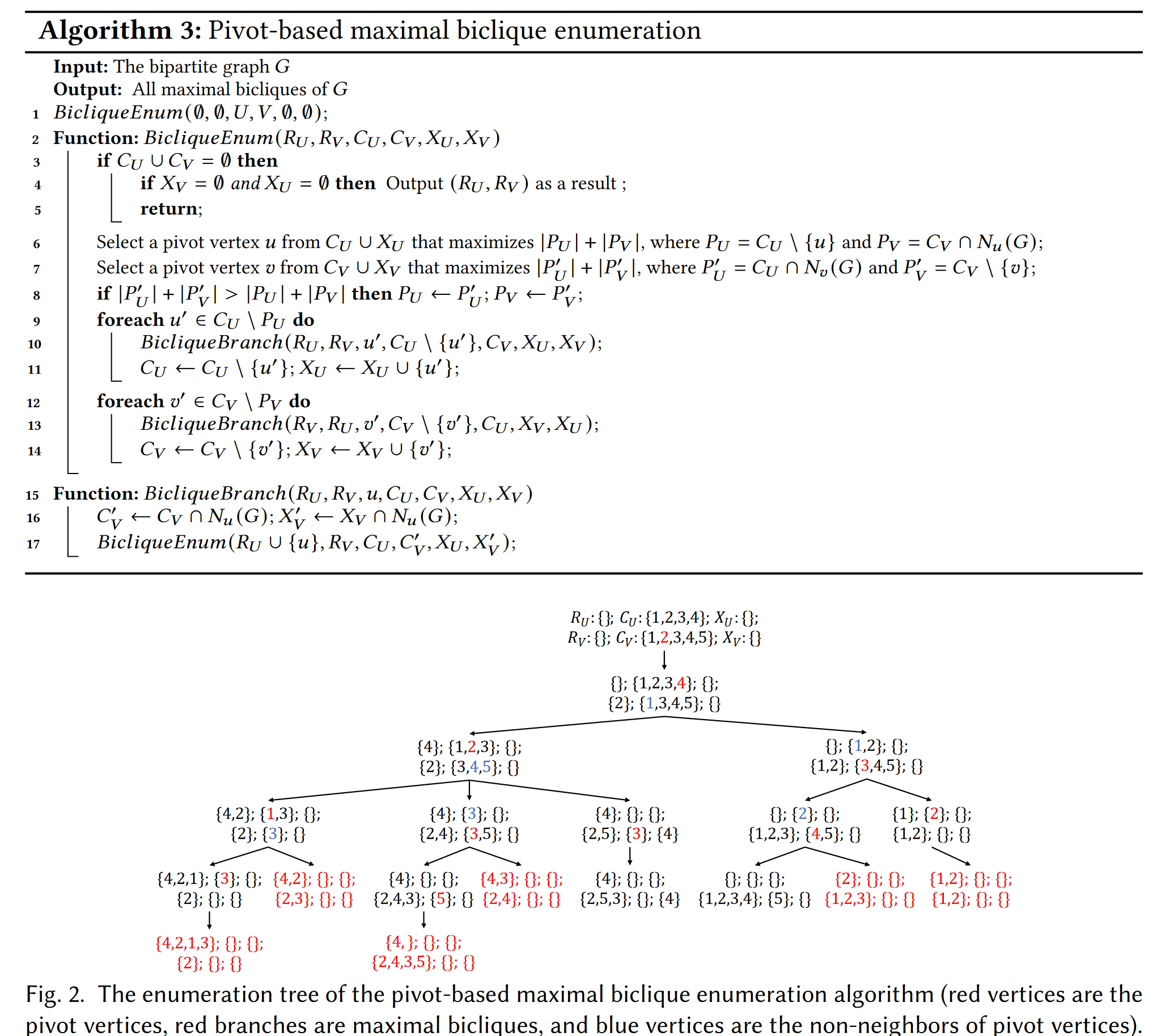
PMBE算法及算法示例图:
复杂度分析:
在选择了pivot后,每一次会产生$|\overline{N}(u)|$+1个分支
假设平均下会产生k+1个分支,也就是说$min{\overline{d_u}(C_V),\overline{d_v}(C_U)=k$
假设选择了$u\in C_U$为pivot,我们可以得到下面的时间的递归式:
$T(n)\le T(n-k-1)+\sum_{i=1}^{k}T(n-k-i)$
如果$u\in X_U$:
$T(n)\le \sum_{i=1}^{k}T(n-k-i)$
第一个分支,候选集合最少减少 k-1个点
后面的k个分支,候选集合减少k-i个点,i代表分支,k指的是后续的剪枝,因为每个v侧的顶点的非邻居数都要大于等于k,这些非邻居都会被剪掉
而且明显$u\in C_U$的时候是worst case,所以只分析第一个式子
- $k=0$:$T(n)=T(n-1)$, constant
- $k=1$: $T(n)\le T(n-1-1)+T(n-1-1)=2T(n-2)$, 递推下去,$T(n)=O(2^{n/2})$
- $k=2$: $T(n)\le T(n-2-1)+\sum_{i=1}^2T(n-2-i)=2T(n-3)+T(n-4)$ ,这个式子比较难推导,但是有个关键的公理:对于一个线性递推式子 $F(n)=\sum_{i=1}^jF(n-a_i)$, $F(n)$ is bounded by $O(\alpha^n)$, and $\alpha$ is the maximum real root of the equation $x^n-\sum_{i=1}^jx^{n-a_i}=0$。所以我们可以退出 $T(n)\le 2^(n/2)$
- $k\ge3$: $T(n)\le T(n-k-1)+\sum_{i=1}^{k}T(n-k-i) \ \le (k+1)T(n-k-1)\=(k+1)^{\frac{n}{k+1}}T(n-(k+1)\cdot\frac{n}{k+1})$ 考虑到 $x^{n/x}$当$x\ge4$的时候单调递增,可以得到$T(n)=O(4^{n/4})=O(2^{n/2})$
5.3 Polynamial-delay Implementation
主要变化就几点:
- 在分支的时候不输出结果
- 在分支内,更新$C$和$X$后,判断把对侧顶点的候选集合全部加上去,是否是个极大biclique,是的话,就输出作为结果
- 如果$C_V$中的点不是$C_U$中点的邻居,就删掉。(避免和第二点的判断做出冗余操作)
核心就是,从初始到第一个结果,需要耗费$m\Delta_{clq}$的时间,$\Delta_{clq}$个顶点,每个点做biclique检查的时间肯定不超过$m$, 然后每次找剩下的结果肯定不会超过n个点,所以每个结果输出间隔肯定是 $nm\Delta_{clq}$
(ps: 其实感觉似乎没啥用)
5.5 优化策略
提前终止策略:$u$为pivot:如果$P_V$为空,那么只需要检查$R_U\cup C_U$,$R_V$是不是maximal biclique 就行。
顶点排序:假设有个顶点的顺序,正常情况下,开启分支限界算法时,是整张图,候选集合也是所有顶点,使用嵌入式子图时,对每个顶点的二跳子图开启分支限界算法,而有了顶点顺序后,可以对每个顶点的高顺序二跳子图开启分支限界算法,这样就避免了重复。理论上应该对X要做特殊设置,否则找的就不是极大的了.
6. Maximal Biplex Enumeration
6.1 Pivot rule of MBPE
假设$u\in C_U\cup X_U$
- $P_V=C_V\cap N(u)$, 虽然biplex可能会遍历到u的非邻居,但是u的邻居肯定会被遍历,所以$P_V$仍然可以这么设置,但是对于biplex而言,这样设置肯定没有biclique那么完美了。
- $P_U$不能和biclique一样,是因为,对于biclique而言,当后续的结果不包含$u$, 也不包含$\overline{N}(u)$的时候,那没有任何$C_U\setminus{u}$以外的点可以包含了(因为本身$C_U$里的点肯定和$R_V$全连接,如果不包含$\overline{N}(u)$,那$u$肯定可以加进去构成新的biclique)。而对于biplex而言,当后续的结果不包含u, 也不包含$\overline{N}(u)$的时候,仍然可能加入$C_U\setminus{u}$中的点,因为biplex的定义。所以要么修改$P_V$的规则,要么修改$P_U$的规则,本文选择修改$P_U$的规则。
- $P_U={w\in C_U | \overline{N}(R_V)\subseteq N_w(G), w\neq v }$,虽然不一样,但是仍然是那个逻辑,如果当前RCX下,$u$为pivot,后续的任何结果(A,B),既不包含$u$, 也不包含$\overline{N}(u)$, 那么肯定A中有个点$v$既不是u的邻居且已经丢失了k条连接,否则肯定可以把u加进去,那么这种情况下,后续的结果里$U$侧肯定要有这个点$v$的邻居,因为$v$不能再接受损失邻居了。所以跳过集合设置成$R_V$中$u$的非邻居的共同邻居(其实理想情况下,应该是$R_V$中$u$的非邻居中已经丢失k条连接的点的共同邻居,但是可能是为了方便计算?感觉和$P_V$一样,也不是特别完美,不过可能是能实现的最好的了?)
- 其实我个人觉得,如果修改pivot的选择规则,也可以更好的制定$P_V$和$P_U$,就是更细粒度一点区分一下pivot的分类,而且,如果可以区别一下问题,枚举大型完整的biplex,那么就更好了,因为这样的话就可以确保biplex内所有的点必为二跳邻居。
6.2 Others
PMBPE 算法:
- 算法6的复杂度是$O(kn)$,比较直接,不做推理
- 算法5的worst time compelxity 是$O(n^22^n)$, 说最差情况下是$2^n$个分支,但是我感觉不对,$P_U$可能没有,但是$P_V$应该是有的
- 后面补了两个枚举大型biplex的优化策略,实际上就是 2-hop剪枝、core、和度数剪枝(deg>|size|-2k)